博观而约取，厚积而薄发

刷题记录--滑动窗口相关

Posted on Edited on In , , Valine: | 置顶 |
Symbols count in article: 2.8k Reading time ≈ 3 mins.

209. 长度最小的子数组

难度中等1393收藏分享切换为英文接收动态反馈

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

1
2
3
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

1
2
输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

1
2
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

  • 1 <= target <= 109
  • 1 <= nums.length <= 105
  • 1 <= nums[i] <= 105

进阶：

  • 如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

解法1:暴力解法，两个循环遍历时间复杂度O(n^2)

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def minSubArrayLen(self, s: int, nums: List[int]) -> int:
        # 定义一个无限大的数
        res = float("inf")
        Sum = 0
        index = 0
        for i in range(len(nums)):
            Sum += nums[i]
            while Sum >= s:
                res = min(res, i-index+1)
                Sum -= nums[index]
                index += 1
        return 0 if res==float("inf") else res

解法2: 滑动窗口参见Carl

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环 完成了一个不断搜索区间的过程。首先要思考 如果用一个for循环，那么应该表示 滑动窗口的起始位置，还是终止位置。

如果只用一个for循环来表示 滑动窗口的起始位置，那么如何遍历剩下的终止位置？此时难免再次陷入 暴力解法的怪圈。

所以 只用一个for循环，那么这个循环的索引，一定是表示 滑动窗口的终止位置。那么问题来了， 滑动窗口的起始位置如何移动呢？这里还是以题目中的示例来举例，s=7， 数组是 2，3，1，2，4，3，来看一下查找的过程：

209.长度最小的子数组

最后找到 4，3 是最短距离。

其实从动画中可以发现滑动窗口也可以理解为双指针法的一种！只不过这种解法更像是一个窗口的移动，所以叫做滑动窗口更适合一些。

在本题中实现滑动窗口，主要确定如下三点：

  • 窗口内是什么？
  • 如何移动窗口的起始位置？
  • 如何移动窗口的结束位置？

窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。解题的关键在于 窗口的起始位置如何移动，如图所示：

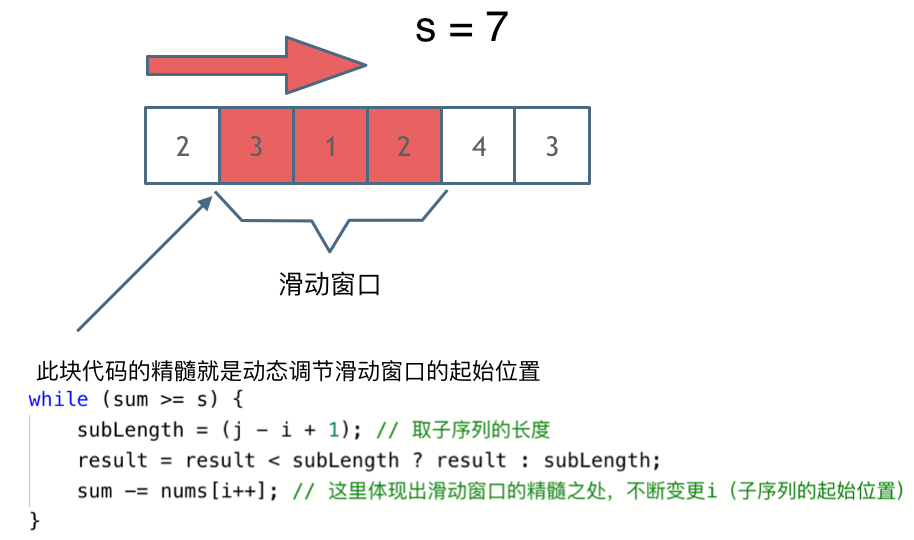
可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#滑动窗口
class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        if nums is None or len(nums)==0: 
            return 0 
        lenf=len(nums)+1
        total=0
        i=j=0
        while (j<len(nums)):
            total=total+nums[j]
            j+=1
            while (total>=target):
                lenf=min(lenf,j-i)
                total=total-nums[i]
                i+=1
        if lenf==len(nums)+1:
            return 0
        else: 
            return lenf

904. 水果成篮

难度中等277收藏分享切换为英文接收动态反馈

你正在探访一家农场，农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示，其中 fruits[i] 是第 i 棵树上的水果 种类 。

你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：

  • 你只有 两个 篮子，并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
  • 你可以选择任意一棵树开始采摘，你必须从 每棵 树（包括开始采摘的树）上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到下一棵树，并继续采摘。
  • 一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。

给你一个整数数组 fruits ，返回你可以收集的水果的 最大 数目。

示例 1：

1
2
3
输入：fruits = [1,2,1]
输出：3
解释：可以采摘全部 3 棵树。

示例 2：

1
2
3
4
输入：fruits = [0,1,2,2]
输出：3
解释：可以采摘 [1,2,2] 这三棵树。
如果从第一棵树开始采摘，则只能采摘 [0,1] 这两棵树。

示例 3：

1
2
3
4
输入：fruits = [1,2,3,2,2]
输出：4
解释：可以采摘 [2,3,2,2] 这四棵树。
如果从第一棵树开始采摘，则只能采摘 [1,2] 这两棵树。

示例 4：

1
2
3
输入：fruits = [3,3,3,1,2,1,1,2,3,3,4]
输出：5
解释：可以采摘 [1,2,1,1,2] 这五棵树。

提示：

  • 1 <= fruits.length <= 105
  • 0 <= fruits[i] < fruits.length

76. 最小覆盖子串

难度困难2175收藏分享切换为英文接收动态反馈

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

  • 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
  • 如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

1
2
输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"

示例 2：

1
2
输入：s = "a", t = "a"
输出："a"

示例 3:

1
2
3
4
输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

提示：

  • 1 <= s.length, t.length <= 105
  • s 和 t 由英文字母组成

进阶：你能设计一个在 o(n) 时间内解决此问题的算法吗？