博观而约取，厚积而薄发

刷题记录--二分查找相关相关

Posted on Edited on In , , Valine: | 置顶 |
Symbols count in article: 5.6k Reading time ≈ 5 mins.

刷题记录

二分查找相关题目汇总

704. 二分查找

难度简单1001收藏分享切换为英文接收动态反馈

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

1
2
3
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

1
2
3
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

  1. 你可以假设 nums 中的所有元素是不重复的。
  2. n 将在 [1, 10000]之间。
  3. nums 的每个元素都将在 [-9999, 9999]之间。

解析，两种方法，注意区间闭合情况，共三处不同，right初始值，while循环条件和right赋值情况(要简略就三个条件都简略，没有➖1没有等于) 复杂度n log n

  1. 区间左闭右开

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    def search(nums, target):
        left, right = 0, len(nums) 
        
        while left < right:
            middle = (left + right) // 2

            if nums[middle] < target:
                left = middle + 1
            elif nums[middle] > target:
                right = middle
            else:
                return middle
        return -1

    # nums = [-1,0,3,5,9,12]
    # target = 2

    nums = [-1,0,3,5,9,12]
    target = 9
    # search(nums,5)
    print(search(nums,target))

  2. 区间左闭右闭

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    def search(nums, target):

        left, right = 0, len(nums) - 1
        while(left <= right):
            mid = (left + right) // 2 
            if (nums[mid] < target):
                left = mid + 1
            elif (nums[mid] > target):
                right = mid - 1
            else:
                return mid 
        return -1

35. 搜索插入位置

难度简单1734收藏分享切换为英文接收动态反馈

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

1
2
输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

1
2
输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

1
2
输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

  • 1 <= nums.length <= 104
  • -104 <= nums[i] <= 104
  • nums 为 无重复元素 的 升序 排列数组
  • -104 <= target <= 104

题解：本质还是二分查找，⚠️二分查找没找到结果，一定是下面代码中left = right时跳出循环，故直接返回即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def searchInsert(nums, target):
    left = 0
    right = len(nums) 
    while(left < right):
        mid = (left + right) // 2
        if(nums[mid] < target):
            left = mid + 1 
        elif (nums[mid] > target):
            right = mid
        else:
            return mid
    return right

nums = [1,3,5,6]
target = 2
print(searchInsert(nums, target))

34. 在排序数组中查找元素的第一个和最后一个位置

难度中等1929收藏分享切换为英文接收动态反馈

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

1
2
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

1
2
输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

1
2
输入：nums = [], target = 0
输出：[-1,-1]

提示：

  • 0 <= nums.length <= 105
  • -109 <= nums[i] <= 109
  • nums 是一个非递减数组
  • -109 <= target <= 109

题解：三种解法：

解法一：两个二分搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] res=new int[2];
        if(nums.length==0||nums==null) return new int[]{-1,-1};
        res[0] = findFirst(nums, target);
        res[1] = findLast(nums, target);
        return res;
    }

    private int findFirst(int [] nums, int target){
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] == target) {
            // 别返回，锁定左侧边界
                right = mid - 1;
            }
        }
    // 最后要检查 left 越界的情况
        if (left >= nums.length || nums[left] != target)
            return -1;
        return left;
    }

    private int findLast(int [] nums, int target){
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] == target) {
            // 别返回，锁定右侧边界
                left = mid + 1;
            }
        }
    // 最后要检查 right 越界的情况
    if (right < 0 || nums[right] != target)
        return -1;
    return right;
    }
    
     
}

解法二：一个二分搜索，然后左右微调滑动窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution(object):
    def searchRange(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        
        def biarySearch(nums,target):
            left, right = 0, len(nums)
            while(left < right):
                mid = (left + right) // 2
                if (nums[mid] > target):
                    right = mid 
                elif (nums[mid] < target):
                    left = mid + 1 
                else:
                    return mid 
            return -1
        index = biarySearch(nums,target)
        left,right = index,index
        if index == -1:
            return([-1,-1])
        while left -1 >= 0 and nums[left - 1] == target :
            left -= 1
        while right+1 < len(nums) and nums[right+1] == target:
            right += 1
        return [left,right]

解法三：没看懂？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 1、首先，在 nums 数组中二分查找得到第一个大于等于 target的下标leftBorder；
# 2、在 nums 数组中二分查找得到第一个大于等于 target+1的下标， 减1则得到rightBorder；
# 3、如果开始位置在数组的右边或者不存在target，则返回[-1, -1] 。否则返回[leftBorder, rightBorder]
class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        def binarySearch(nums:List[int], target:int) -> int:
            left, right = 0, len(nums)-1
            while left<=right: # 不变量：左闭右闭区间
                middle = left + (right-left) //2 
                if nums[middle] >= target: 
                    right = middle - 1
                else: 
                    left = middle + 1
            return left  # 若存在target，则返回第一个等于target的值 

        leftBorder = binarySearch(nums, target) # 搜索左边界
        rightBorder = binarySearch(nums, target+1) -1  # 搜索右边界
        if leftBorder == len(nums) or nums[leftBorder]!= target: # 情况一和情况二
            return [-1, -1]
        return [leftBorder, rightBorder]

69. x 的平方根

难度简单1154收藏分享切换为英文接收动态反馈

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

1
2
输入：x = 4
输出：2

示例 2：

1
2
3
输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

提示：

  • 0 <= x <= 231 - 1

解法一：二分法，注意边界条件，注意循环终止条件，还像之前用左开右闭区间的话，缺少=条件，例如x=0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution(object):
    def mySqrt(self, x):
        """
        :type x: int
        :rtype: int
        """
        left, right = 0, x 
        ans = -1
        while(left <= right):
            mid = (left + right) // 2 
            if (mid * mid <= x):
                ans = mid
                left = mid + 1 
            else:
                right = mid -1
        return ans

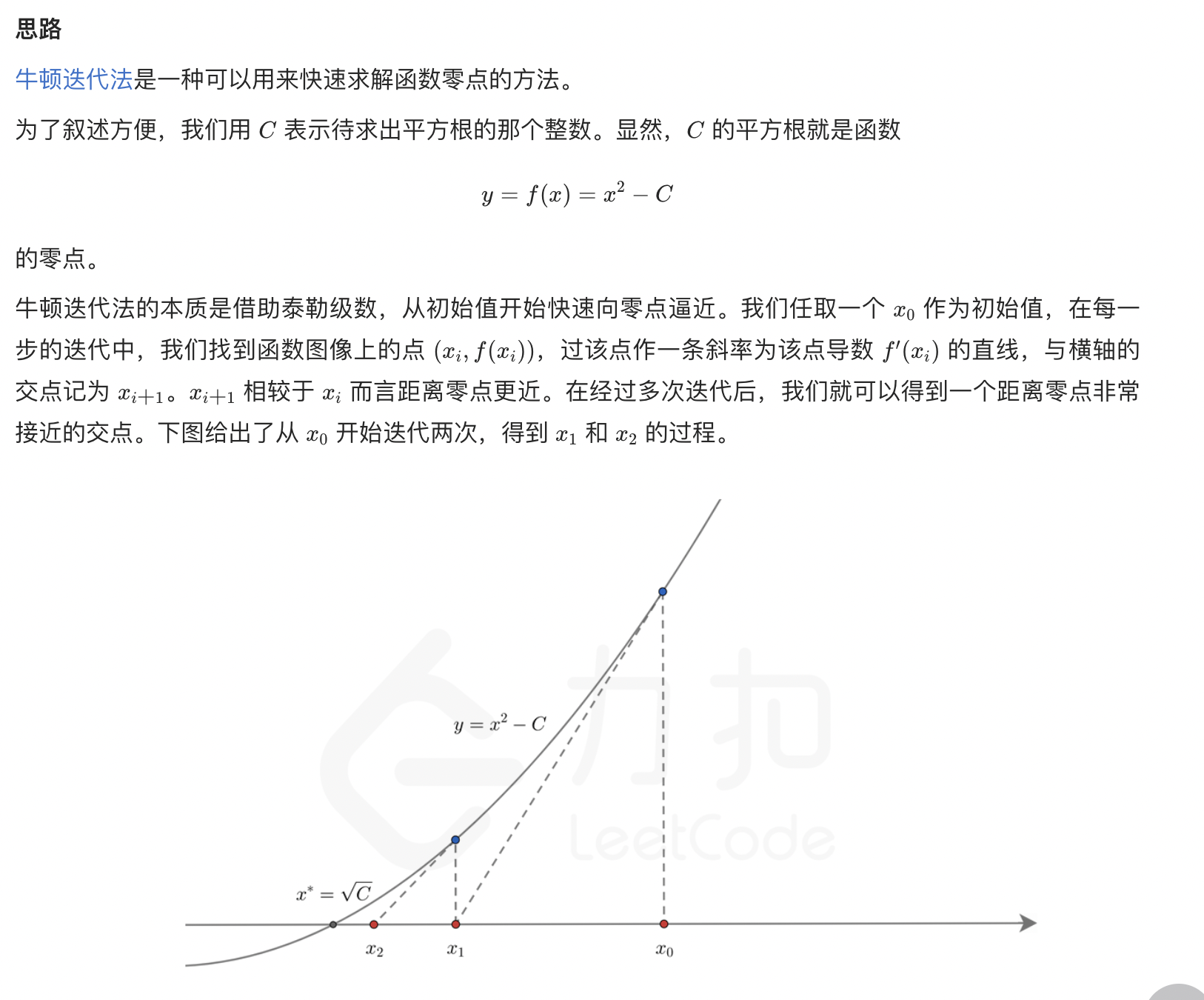
解法二：牛顿迭代法

image-20221001164722493

image-20221001164811043

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def mySqrt(self, x: int) -> int:
        if x == 0:
            return 0
        
        C, x0 = float(x), float(x)
        while True:
            xi = 0.5 * (x0 + C / x0)
            if abs(x0 - xi) < 1e-7:
                break
            x0 = xi
        
        return int(x0)

367. 有效的完全平方数

难度简单439收藏分享切换为英文接收动态反馈

给定一个 正整数 num ，编写一个函数，如果 num 是一个完全平方数，则返回 true ，否则返回 false 。

进阶：不要 使用任何内置的库函数，如 sqrt 。

示例 1：

1
2
输入：num = 16
输出：true

示例 2：

1
2
输入：num = 14
输出：false

提示：

  • 1 <= num <= 2^31 - 1

题解：跟上题一样，两种解法，二分查找或者牛顿迭代

二分查找，有mid就返回true，没有就返回false

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution(object):
    def isPerfectSquare(self, num):
        """
        :type num: int
        :rtype: bool
        """
        left, right = 0, num 
        while (left <= right):
            mid = (left + right) // 2
            if (mid * mid < num):
                left = mid + 1
            elif (mid * mid > num):
                right = mid - 1
            else:
                return True
        return False

牛顿迭代，返回计算的int(x)平方是否等于num

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution(object):
    def isPerfectSquare(self, num):
        """
        :type num: int
        :rtype: bool
        """
        x0,C = float(num),float(num)
        while(True):
            xi = 0.5*(x0+C/x0)
            if (abs(x0-xi)< 1e-7):
                break 
            x0 = xi 
        return int(x0)*int(x0)==num